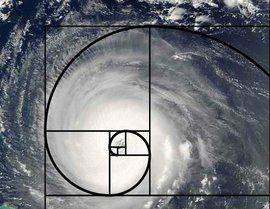
发现数学之美—斐波那契数列 学过高中数列的应该有些听过，咋一看感觉是个很普通的数列，但其实非常有意思。斐波那契数列，就是第0项a0等于0，第一项a1等于1，后面的每一项都等于前两项相加，依次类推。稍微列几个就是0，1，1，2，3，5，8，13，21，34……把它的通项公式写出来就是下图的公式，可以发现所有斐波那契数都是有理数，但是通项公式却是用到无理数表示的。有兴趣的自己可以代入算下。 当我们把斐波那契数列的每前一项都除以后一项，比如1÷2＝0.5，2÷3＝0.666，5÷8＝0.625，8÷13＝0.615，21÷34＝0.617，发现了什么，n越来越大的时候，a(n－1)除以an的比值越接近黄金分割率0.618，事实上当n趋于无穷大时，他的比值就是黄金分割率。 大自然中，很多植物花瓣的数量，螺纹的排列，树枝分叉的数目，都属于斐波那契数。下图二是斐波那契螺旋线，里面每个正方形的边长都属于斐波那契数，从而做出的螺旋线具有非常的美感。在艺术创造，建筑，摄影构图等等方面都可以找到应用的场景。

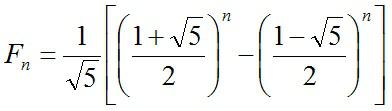
评论：