用户:对方正在长头发
2025-02-23 17:02:58 晴
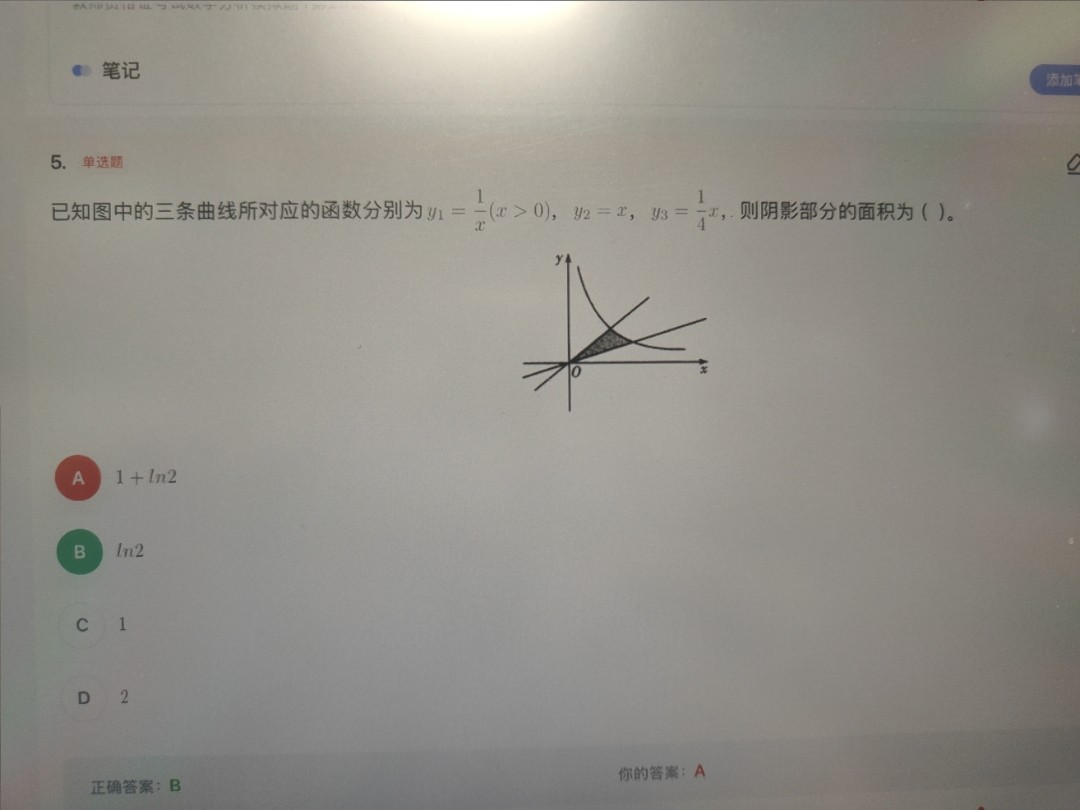
随可以帮我讲讲这一题,定积分面积类的题脑子浑浑的…[感动]
#微积分 #数学大佬救救我这个孩子吧 >>阅读更多
用户:🍰
2025-03-04 20:33:35 晴
谁愿意教教我定积分啊啊啊#高数 #微积分 >>阅读更多
用户:airplane
2025-03-17 09:59:41 晴
谁来教我概率论呢?#概率论与数理统计 #求带概率论 #微积分 >>阅读更多
用户:撸铁的地场卫
2025-03-10 10:29:58 晴
天气好,同学们来做个题庆祝一下🎉🎉🎉#高数 #罗尔定理 #微积分 >>阅读更多

用户:Stella.
2025-03-29 20:13:47 晴
谁能给我讲讲二重积分和微分方程和多元函数微分学[捂脸哭][捂脸哭]#微积分 #高数 #大佬带我高数! >>阅读更多
用户:那我问你
2025-02-27 01:43:30 晴
#概率论 #求概率论大神 #求带概率论 #概率论与数理统计 #概率论与数理统计 #概率论与数理统计 #概率论与数理统计 #概率论与数理统计 #概率论与数理统计 #概率论与数理统计 #概率论与数理统计 #请教一下概率论与数理统计 #概率论与数理统计 #请教一下概率论与数理统计 #概率论与数理统计 #请教一下概率论与数理统计 #微积分 #概率论与数理统计 #请教一下概率论与数理统计 #概率论与数理统计 #概率论与数理统计 >>阅读更多
用户:回忆梦境星空
2025-01-24 05:08:35 晴
有没有朋友有兴趣弄微积分学习笔记的(latex排版),有的话可以私我哦[可爱]#微积分 #latex >>阅读更多
用户:星空
2025-03-13 09:56:29 晴
第184号文明在“三日连珠”的引力叠加中毁灭了,该文明进化至科学革命和工业革命。
这次文明中,牛顿建立了低速状态下的经典力学体系,同时,由于微积分和冯·诺伊曼结构计算机的发明,奠定了对三体运动进行定量数学分析的基础。
漫长的时间后,生命和文明将重新启动,再次开始在三体世界中命运莫测地进化。
#《三体》#三体书摘#生命文明的进化#力学体系#微积分#计算机#数学分析的基础 >>阅读更多

用户:嘀嗒嘀嗒
2021-09-07 22:31:00 晴
关于严格贯彻11点入眠指导意见...#拖延症晚期 #早睡 #微积分 >>阅读更多



